소개
가장 흔하게 사용하는 loss fuction 중 하나가 Cross Entropy Loss가 아닐까합니다. 대부분의 Deep Learning 프레임워크에서 기본적으로 제공해주기도 하고요. 자주 쓰기는 하지만 Cross Entropy가 실제로 무엇인지 궁금하신 분들도 있을 것 같습니다. 오늘은 Cross Entropy에 대해서 소개를 해보고자 합니다.
스포일러
Cross Entropy는 Information Theory라는 학문에서 나온 개념입니다. 오늘 글에서는 Information Theroy 이야기를 여기저기에서 하게 될 것입니다. 그런데 Machine Learning에서 Cross Entropy를 사용하는 목적은 원래 Information Theory에서 Cross Entorpy를 만든 목적과 다릅니다. 아래에서 다루게 되겠지만 Cross Entropy는 Entropy라는 개념에서 나왔고, Entropy라는 개념을 이해하기 위해서는 다시 Information이라는 수학적 정의를 알아야합니다. 하지만 이 모든 것들이 솔직해 말해 Machine Learning에서는 크게 관계가 없습니다.
Machine Learning 관점에서는 두 데이터(확률 분포) 사이의 Cross Entropy를 계산하면, 두 데이터 사이의 차이를 수치로 표현할 수 있다는 것에 관심이 있습니다. 즉, Cross Entropy는 Loss Fuction이 될 수 있다만 알면 충분합니다. 너무 과하게 단순화시킨 면도 있지만요.
그럼에도 불구하고 Cross Entropy가 도대체 무엇인지, 이론적 배경이 무엇인지 궁금하다면 아래 글을 계속 읽어나가시면 됩니다.
Entropy가 뭐야
Cross Entropy를 이야기하려면 아무래도 Entropy에 대해서 이야기를 먼저 해야할 것 같습니다. 물론 Cross에 대해서도 나중에 이야기합니다.
Entropy에 대해 이야기하려면 Information Theory라는 분야를 이야기해야합니다. 불행히도 Information Theory는 수많은 수학적 정의와 수식들로 이루어져있습니다. 오늘 이 글은 Cross Entropy에 대한 개념을 소개하는 것이 목적이기 때문에 가능한 수식은 피하려고 합니다. 최대한 개념 위주로 이야기를 진행해보겠지만 필수적인 부분에서는 수식이 등장하기도 합니다.
Information
Entropy를 이야기하려면 먼저 Information Theory에서 말하는 Information 이라는 개념을 이야기해야합니다.Information Theory에서 말하는 Information은 어떤 사건을 표현하기 위해 필요한 Bit 수입니다. 예를 들어보겠습니다.
가상의 언어가 하나 있다고 가정해보겠습니다. 이 언어는 아주 단순해서 단어가 A, B, C, D 네가지 밖에 없습니다. 컴퓨터는 숫자 밖에 모르기 때문에 A, B, C, D에 숫자를 하나씩 할당해주어야합니다. A, B, C, D를 숫자로 표현하려면 어떻게 하면 될까요?
A는 0(2진수로는 00), B는 1(01), C은 2(10), D는 3(11)라고 하면 아주 직관적입니다. 제가 "0 1 2 0 0 3 0 1 2 0 "이라고 보내면 받는 쪽에서 "A B C A A D A B C A"라고 한거구나라고 해석하겠죠. 이 언어를 표현하는데는 총 2비트만 있으면 됩니다.
1번 코딩 방식
| 단어 | 2진수 코드 |
|---|---|
| A | 00 |
| B | 01 |
| C | 10 |
| D | 11 |
그런데 가만히 이 언어를 쓰는 사람들을 관찰해보니 A 단어는 많이 쓰는데 D는 잘 안 씁니다. 사람들이 쓰는 말을 잘 관찰해서 아래와 같은 확률 데이터 얻습니다.
| 단어 | 확률 |
|---|---|
| A | 0.5 |
| B | 0.2 |
| C | 0.2 |
| D | 0.1 |
그리고 잘 생각해보니 D는 10번 중에 1번만 쓰는데 똑같이 2비트를 쓰는 것이 왠지 낭비같습니다. "A B C A A D A B C A"라고 보낸다고 치면 무조건 단어마다 2비트이기 때문에 총 20비트가 필요합니다.
만약에 자주 쓰는 단어는 적은 비트 수를 쓰고, 자주 안 쓰는 단어는 좀 많은 비트 수를 쓰면 전체적으로는 적은 비트 수를 쓸 수 있지 않을까요? 아래와 같이 코드를 바꿔봅니다.
2번 코딩 방식
| 단어 | 2진수 코드 |
|---|---|
| A | 0 |
| B | 10 |
| C | 11 |
| D | 111 |
이제 "A B C A A D A B C A"는 "0 10 11 0 0 111 0 01 10 0"으로 쓸 수 있습니다. 총 16비트를 사용했습니다. 가장 긴 경우에 3비트를 쓰기는 하지만 전체적으로는 원래 방식보다 무려 20%를 절약했습니다.
1번 코딩 방식에서는 이 새로운 언어를 표현하는데 2비트를 사용했습니다. 각 단어를 사용할 확률이 똑같다고 생각했기 때문입니다. 2번 코딩 방식에서는 최대 3비트를 사용합니다. 특정 단어를 사용할 확률이 더 많다는 정보(Information)를 알았기 때문에 이를 이용해서 더 효율적인 코딩 방식을 만들었습니다.
Information을 수학적으로는 -log(p(x))로 정의합니다. 모든 단어를 똑같은 확률로 사용한다고 가정한 경우 Information 값은 아래와 같습니다.
| 단어 | 확률 | Information |
|---|---|---|
| A | 0.25 | 2.0 |
| B | 0.25 | 2.0 |
| C | 0.25 | 2.0 |
| D | 0.25 | 2.0 |
모든 단어가 같은 Information을 갖습니다. Information은 어떤 사건을 표현하기 위해 필요한 Bit 수라고 했는데 이 정의에 따르면 각 단어별로 2 Bit를 써야합니다.
이번에는 단어별로 확률이 다른 경우를 살펴보겠습니다.
| 단어 | 확률 | Information |
|---|---|---|
| A | 0.5 | 1.0 |
| B | 0.2 | 2.3 |
| C | 0.2 | 2.3 |
| D | 0.1 | 3.3 |
A의 Information이 가장 낮고, D의 Information이 가장 높습니다. Bit 수로 따지자면 A를 표현하는데는 1 Bit를 쓰면 되고, D를 표현하기 위해서는 약 3 Bit를 쓰면 됩니다. 우리가 정한 B 코딩 방식과 비슷하네요.
Information을 통해 알 수 있는 것은 필요한 Bit 수 외에도 Surprise라는 개념이 있습니다. 특정 사건이 실제로 일어났을 때 얼마나 놀라울까를 표현한 것입니다.
예를 들어 상대방이 이 가상의 언어로 이야기를 하고 있다고 생각해보겠습니다. 상대방이 "A"라고 말하면 별로 놀라지 않을 겁니다. 많이 듣던 말이니까요. 그런데 갑자기 이 사람이 "D"라고 합니다. 오호?하고 잠이 깨면서 상대방의 말에 집중하게 될 것입니다. 자주 듣지 않던 말이니까요. 즉, A는 Suprise하지 않지만 D는 Surprise합니다.
왜 우리는 D라는 단어를 들으면 더 관심이 가고 Surprise할까요? 바로 자주 일어나지 않는 일이고 무엇인가 새로운 정보(Information)을 담고 있을 가능성이 높기 때문입니다. 바로 아래와 같이 말할 수 있습니다.
- 높은 확률 -> 뻔하다 -> Information이 적다/낮다
- 낮은 확률 -> 신선하다 -> Information이 많다/높다
Entropy
Entropy의 정의는 어떤 확률 분포를 표현하는데 필요한 Bit 수입니다. Information이 특정 사건을 표현하기 위한 Bit 수였다면, Entropy는 확률 분포 전체를 표현하기 위한 Bit 수입니다.
다른 설명 방법도 있습니다. Entropy는 어떤 일이 일어날 가능성이 확실한지, 불확실한지를 수치로 표현한 것입니다. 오늘 하루 동안 저는 밥을 먹을까요 안 먹을까요? 아마도 높은 확률로 밥을 먹을 겁니다. 제가 오늘 밥을 먹을 것은 확실하죠. 그래서 제가 오늘 밥을 먹는 사건은 낮은 Entropy를 가집니다.
제가 내일 로또에 당첨되는 일은 어떨까요? 아주 낮은 확률을 가질 것입니다. 슬픈 일이지만 거의 확실하죠. 제가 내일 로또에 당첨될 사건도 낮은 Entropy를 가집니다.
다른 예로 100원 짜리 동전을 던진다고 생각해보겠습니다. 이순신 장군이 나올까요, 숫자 100이 나올까요. 음... 이건 잘 모르겠습니다. 확률이 거의 반반이니까요. 이순신 장군을 보게 될지, 숫자 100을 보게 될지는 불확실합니다. 즉, 높은 Entropy를 가집니다.
- 내일 A라는 일이 확실히 일어날거야: 낮은 Entropy
- 내일 B라는 일은 확실히 안 일어날거야: 낮은 Entropy
- 내일 C라는 일이 일어날지 안 일어날지 감이 잘 안 오는데: 높은 Entropy
확률 vs Entropy
이렇게 되면 확률과 Entropy가 헷갈릴 수 있습니다. 확률은 특정 사건이 일어날지 안 일어날지를 수치로 표현한 것입니다. Entropy 그 사건의 불확실성을 수치로 표현한 것입니다. 말이 복잡하네요. 예를 들어 살펴보겠습니다.
추첨을 통해 경품을 주는 행사가 있습니다. 1등은 최신형 핸드폰, 2등은 스마트 워치, 3등은 커피 쿠폰입니다.
상자 A에는 1등 종이가 1개, 2등 종이가 2개, 3등 종이가 7개 들어있습니다. 상자 B에는 1등 종이 3개, 2등 종이 3개, 3등 종이 4개가 들어있습니다. 두 상자 모두 총 10개의 종이가 들어있습니다.
상자 A의 경우,
- 1등 당첨 확률은 1/10
- 2등 당첨 확률은 2/10
- 3등 당첨 확률은 7/10
입니다.
상자 B의 경우,
- 1등 당첨 확률은 3/10
- 2등 당첨 확률은 3/10
- 3등 당첨 확률은 4/10
입니다.
상자 A에서 1등이 될 확률(1/10)보다 상자 B에서 1등이 될 확률(3/10)이 훨씬 높습니다.
Entropy는 어떨까요? 어떤 상자가 더 불확실한가요? 다르게 말하면 첫 추첨을 했을 때 1등이 나올지, 2등이 나올지, 3등이 나올지 어떤 상자가 더 예측하기 어렵나요? B일 것입니다. 상자 A는 3등이 나올 확률이 7/10으로 1등(1/10)이나 2등(2/10)보다 압도적으로 높습니다. 상자 A에서 뽑는다면 대부분 사람들은 첫 뽑기 결과가 3등일 것이라고 예상할 겁니다. 불확실성이 낮습니다. 낮은 Entropy죠.
반면 B는 어떨까요? 1등, 2등, 3등이 모두 비슷한 확률을 가지고 있습니다. 첫 뽑기 결과를 예측하기가 어렵죠. 스릴이 넘칩니다. 불확싱설이 높습니다. 높은 Entropy죠.
정리해보면 확률은 특정 사건에 대한 수치(1등을 뽑을 확률)입니다. Entropy는 전체 사건에 대한 수치(얼마나 예측이 어렵느냐)입니다.
Entropy 수식
Entorpy의 정의가 어떻게 되는지 수식을 한번 보겠습니다.

여기에서 log는 밑이 2입니다.
Information과 Entropy
이 수식은 다시 쓰면 아래와 같이 쓸 수 있습니다. 앞의 -를 안 쪽으로 넣었습니다.

즉, 각 사건의 Information인 -log(p(x))에 p(x)를 곱한 다음 전체를 더한 것이 Entropy입니다. Entropy 수식에 왜 Information이 들어있을까요? 바로 어떤 사건의 불확실성은 결국 Information과 관련이 있기 때문입니다. 어떤 사건이 너무 뻔하게 일어나거나(1에 가까운 확률) 뻔하게 일어나지 않는다면(0에 가까운 확률) 우리가 얻을 수 있는 Information이 있을까요? 없습니다. 뻔하다 -> 놀라움이 없다 -> Information 없다. 반면 어떤 사건이 일어날지 일어나지 않을지 예측하기 어렵다면 Information 또한 높습니다.
이어서 더 다루겠지만 이렇게 Entropy와 Information은 밀접한 관계를 가집니다.
-p(x)log(p(x))
이 수식이 어떤 의미를 가질까요? 아래는 -x*log(x)의 그래프입니다.
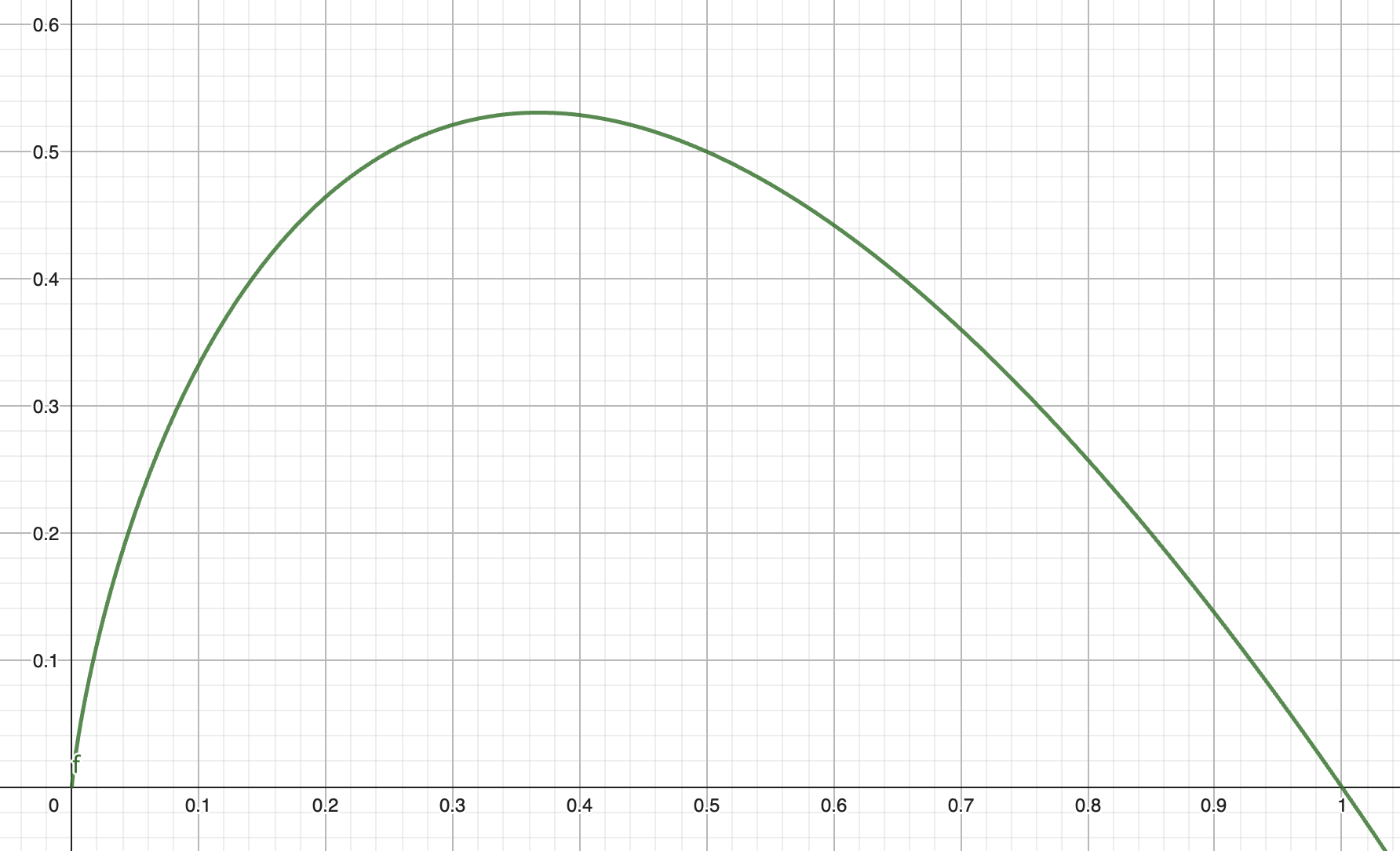
보시면 y가 0에서 시작해 x가 0.35(정확히는 0.368)까지는 y값이 올라가다가(0.531까지 올라갑니다), 그 뒤로 x는 1일 때 다시 0까지 떨어지는 것을 볼 수 있습니다.
y 값은 각 사건이 가진 불확실성으로 해석할 수 있습니다. 어떤 사건이 일어날 확률이 0이라는 말은 이 사건이 확실히 일어나지 않는다는 뜻입니다. 즉, 불확실성은 0입니다. 확률이 1이어도 비슷합니다. 확실히 일어난다는 의미이고 불확실성은 1입니다. 반면, 확률이 0과 1에서 벗어날수록 그 사건이 일어날지 안 일어날지 판단하기 어려워집니다. 즉, 불확실성이 올라가는 셈이죠.
앞의 A 상자에서 1등이 될 확률 p(1등)은 0.1입니다. -p(1등)log(p(1등)) = - 0.1 * p(log0.1) = 0.332입니다.
Entropy 계산
Entropy는 모든 사건에 해당하는 -p(x)log(p(x))를 더한 값입니다. 개념적으로보면 각 사건이 일어날 불확실성을 다 더한 값이 Entropy입니다.
A상자
| 사건 | 확률 | 불확실성 |
|---|---|---|
| 1등 | 0.1 | 0.332 |
| 2등 | 0.2 | 0.464 |
| 3등 | 0.7 | 0.361 |
| 합 | 1.0 | 1.157 |
확률이 0.1인 사건보다는 0.2인 사건의 불확실성이 더 높습니다. 일어날 확률이 0.1 밖에 안 될 때는 "에이 안 되겠네."라는 생각이 들지만, 확률이 0.2가 된다면 "혹시 모르겠는데?"라는 생각이 들긴하죠. 확률이 0.7이 되면 불확실성은 다시 떨어집니다.
1등, 2등, 3등에 대한 불확실성을 다 더한 값이 상자 A의 Entropy입니다. 이 경우에 값은 1.157입니다.
1.157이 무슨 의미일까요? Information Theory에 따르면 A 상자에서 생기는 사건을 전달하기 위해 필요한 Bit 수라고 합니다. 즉, A상자에서 1등, 2등, 3등이 뽑힐 사건을 표현하려면 우리는 1.157 Bit가 필요합니다.
이제 B상자를 살펴보겠습니다. 아래는 B상자를 계산한 결과입니다.
B상자
| 사건 | 확률 | 불확실성 |
|---|---|---|
| 1등 | 0.3 | 0.521 |
| 2등 | 0.3 | 0.521 |
| 3등 | 0.4 | 0.529 |
| 합 | 1.0 | 1.571 |
B상자의 Entropy는 1.571입니다.
A상자의 Entropy가 1.157이고, B상자의 Entropy가 1.571이라는 의미는 무엇일까요? A 상자보다 B 상자의 불확실성이 더 높다는 뜻입니다. 즉, A 상자에서 추첨할 때 보다, B 상자에서 추첨할 때 결과를 더 예측하기 어렵다는 것이죠.
Cross Entropy
Entropy가 무엇인지는 알았습니다. 그럼 이제 Cross 에 대해서 이야기해보겠습니다.
Cross Entropy 역시 Information Theory에서 나온 개념입니다. 실제 데이터는 확률 분포 P(x)에서 나오는데 우리는 이 데이터를 표현하기 위해서 Q(x)라는 다른 확률 분포를 사용한다고 가정해보겠습니다. Q(x)를 통해서 예측한 확률 값은 진짜 확률 값 P(x)와 다르겠죠. Cross Entropy는 실제 P(x)인 데이터를 Q(x)를 사용해서 표현한다면 얼마나 많은 Bit가 필요하느냐를 나타냅니다.
역시 말이 어렵습니다. 조금 더 살펴보죠.
Cross Entropy는 수식으로 아래와 같습니다.
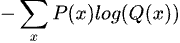
Entropy 시식과 같지만 log(p(x)) 대신 log(q(x))를 사용합니다. Entropy 이지만 한 가지 확률 분포가 아니라 두 확률 분포 사이(Cross)의 Entropy를 계산하기 때문에 Cross Entropy라고 부릅니다.
Entropy와 Cross Entropy
Cross Entropy는 항상 Entropy보다 큽니다. 수학적으로 증명 가능하지만 이 글에서 그 부분은 다루지 않겠습니다. 대신 https://stats.stackexchange.com/questions/370428/why-is-the-cross-entropy-always-more-than-the-entropy 을 참고하시기 바랍니다.
이 글에서는 조금 더 직관적인 해석을 해보려고 합니다.
Cross Entropy (P, Q)는 실제 데이터는 P(x) 분포인데 이를 Q(x) 분포로 표현할 때 얼마나 많은 Bit가 필요한지를 나타내는 값이라고 했습니다. Entropy(P)는 P 분포를 가장 효율적으로 표현할 수 있는 Bit 수입니다. P가 아닌 어떤 분포를 사용하더라도 P보다 더 적은 Bit를 사용할 수는 없습니다. 정의상 이미 P가 가장 효율적인 분포이니까요. 즉, Cross Entropy (P, Q)는 Entropy (P)보다 클 수 밖에 없습니다.
Cross Entorpy (P, Q)가 가장 작아질 때는 언제일까요? 바로 Q가 P와 같을 때 입니다. 그 외에는 항상 Cross Entropy (P, Q) > Entorpy (P) 입니다. 또다른 유용한 특징은 P와 Q가 비슷할 수록 값은 Entropy(P)에 가까워지고, P와 Q가 다를수록 값이 Entropy(P)와 멀어진다는 점입니다.
Loss Function 으로써 Cross Entropy
이런 Cross Entropy의 특성은 Loss Function으로 쓰기에 아주 좋습니다. P는 정답 데이터라고 하고 Q를 우리 모델이 현재 예측하는 데이터라고 해보겠습니다. 모델이 점점 더 정확한 예측을 할 수록 Cross Entropy(P, Q)는 작아질 것입니다. 즉, 우리는 Cross Entropy(정답 데이터, 모델의 예측 값)이 줄어들도록 모델을 훈련시키면 됩니다.
Cross Entropy와 Classification
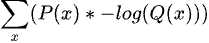
다시 Cross Entropy 수식을 살펴보겠습니다. 앞의 수식과 같지만 앞의 -를 안으로 넣었습니다.
Machine Learning 관점에서 해석해보면,
- p(x) : 훈련 데이터 상 Label의 확률입니다. 정답 Label의 p(x)는 1.0, 다른 Label의 p(x)는 0.0입니다.
- -log(q(x)) : 우리 모델이 예측하는 데이터로 계산하면 됩니다. 우리 모델의 현재 분포에 따른 Information 이겠죠.
예를 들어 어떤 사진을 개, 고양이, 사슴으로 분류하는 모델이 있다고 해보겠습니다. 훈련 데이터는 [개, 고양이, 사진]을 One-hot vector로 표현합니다. 훈련 데이터에 아래와 같이 세가지 인스턴스가 있다고 해보겠습니다.
- x1 -> [1, 0, 0] (개)
- x2 -> [0, 0, 1] (고양이)
- x3 -> [0, 0, 1] (사슴)
첫번째 사진 x1은 개입니다. 예측해야하는 벡터는 [1, 0, 0]입니다. x2, x3도 비슷하게 구성합니다.
현재 우리 모델이 예측한 값은 아래와 같다고 해보겠습니다.
- x1 -> [0.3, 0.2, 0.5] (사슴)
- x2 -> [0.2, 0.7, 0.1] (고양이)
- x3 -> [0.3, 0.4, 0.3] (고양이)
먼저 x1에 대한 Cross Entropy를 계산해보겠습니다. 모든 Label에 대해 -p(x)log(q(x))를 계산하고 더하면 됩니다.
이 중에서 첫번째 부분만 먼저 해보면,
-p(x1_개) * log(q(x1_개)) = -1.0 * log(0.3) = 1.0 * 1.737 이 됩니다.
이제 개, 고양이, 사슴 전체에 대해서 값을 계산합니다.
-p(x1_개) * log(q(x1_개)) + -p(x1_고양이) * log(q(x1_고양이)) -p(x1_사슴) * log(q(x1_사슴))
= 1.0 * 1.737 + 0.0 * 2.322 + 0.0 * 1.000
= 1.737
한가지 특이한 점은 p(x)입니다. log(q(x))가 무엇이 됐든지 정답이 아닌 Label이 p(x)는 0이기 때문에 -p(x)log(q(x))는 결국 0이 됩니다. log(q(x))를 계산할 필요가 없는 셈이죠. 이 때문에 어떤 수식에서는 Cross Entropy를 계산할 때 정답 Label에 대해서만 고려하면 된다고도 합니다.
같은 식으로 x2의 Cross Entropy를 구하면 0.515이고, x3의 Cross Entropy는 1.737입니다. 전체 데이터의 평균 Cross Entropy는 (1.737 + 0.515 + 1.737) / 3 = 1.330 입니다.
훈련 시간이 더 지나서 이제 모델의 예측치가 아래와 같이 바뀌었다고 해보겠습니다.
- x1 -> [0.95, 0.02, 0.03] (개)
- x2 -> [0.05, 0.9, 0.05] (고양이)
- x3 -> [0.05, 0.08, 0.87] (사슴)
같은 방식으로 계산하면 x1의 Cross Entropy는 0.074, x2는 0.152, x3는 0.201입니다. 평균 Cross Entorpy는 0.142입니다. 정확도가 올라간만큼 Cross Entropy의 값도 줄어든 것을 볼 수 있습니다.
그럼 Cross Entropy Loss는 어디까지 작아질 수 있을까요? 답은 0입니다. 모델의 출력값이 훈련 데이터와 같다고 가정하고 계산해보면 됩니다.
- x1 -> [1, 0, 0] (개)
- x2 -> [0, 0, 1] (고양이)
- x3 -> [0, 0, 1] (사슴)
-p(x1_개) * log(q(x1_개)) + -p(x1_고양이) * log(q(x1_고양이)) -p(x1_사슴) * log(q(x1_사슴))
= 1.0 * 0.0 + 0.0 * 무한대 + 0.0 * 무한대
= 0.0
앞에서 Cross Entropy (P, P)의 값은 Entropy (P)와 같다고 했습니다. Cross Entropy (P, P)가 0이 되는 것은 Classification과 같이 특수한 경우에서만 발생합니다. 정답이 아닌 Label의 확률 p(x)가 항상 0이기 때문입니다.
정리
Loss Function으로 자주 사용하는 Cross Entropy에 대해서 알아보았습니다.
- Cross Entropy는 Information Theory 라는 학문에서 나온 개념이다.
- Information Theory에서 Information은 어떤 사건을 표현하기 위해 필요한 Bit수를 의미한다.
- Information은 그 사건이 얼마나 뻔하지 않고 놀라움을 주는지를 표현한다. 많은 Bit가 필요하다 -> 뻔하지 않다 -> 새로운 정보를 담고 있다.
- Entropy는 확률 분포 전체를 표현하기 위해 필요한 Bit 수를 의미한다.
- Information과 비슷하게 Entropy는 어떤 확률 분포가 얼마나 뻔하지 않은지(예측이 어려운지)를 표현한다.
- Cross Entropy는 P 확률 분포를 따르는 데이터를 Q 확률 분포로 표현할 때 필요한 Bit 수를 의미한다.
- P와 Q가 다를수록 Cross Entropy (P, Q)의 값이 커진다. P, Q가 같을 때 Cross Entropy 값이 가작 작다.
- 이런 Cross Entropy의 특성 탓에 P를 훈련 데이터, Q를 모델의 예측 데이터로 설정해 loss를 계산하는 데 사용한다.
단순히 두 데이터(확률 분포) 사이의 차리를 측정하는 값으로 사용하던 Cross Entropy에는 여러가지 이론적인 배경이 있습니다. Cross Entropy에는 Information Theory의 많은 이론이 담겨있지만 솔직히 Machine Learning 관점에서 크게 중요하지는 않을 수 있습니다.우리는 Cross Entropy를 두 데이터 사이의 차이(거리)를 측정하는 도구로 활용하니까요.
하지만 언제나 도구 뒤에 숨은 원리를 아는 것은 좋은 일이라고 생각합니다. 그래야 더 좋은 기술을 개발할 수도 있고, 문제가 생겼을 때 효과적으로 대처를 할 수도 있으니까요.
'Deep Learning' 카테고리의 다른 글
| LLM : RAG (3) | 2024.04.28 |
|---|---|
| LLM : Fine Tuning & LoRA (3) | 2023.11.12 |
| LLM : In-Context Learning, 남은 이야기들 (13) | 2023.04.12 |
| LLM : LLM을 가능케한 삼박자 (8) | 2023.04.12 |
| LLM : Foundation Model (2) | 2023.04.12 |