LLM을 어떻게 훈련시키냐만큼 중요한 것이 LLM을 어떻게 서비스하냐입니다. 얼마나 효율적으로 출력을 만들어 낼 수 있느냐는 Throughput으로 이어지고 결국 비용과 직결됩니다.
초당 100개의 요청을 처리하고 싶은데, 실제로는 초당 10개만 처리할 수 있다면 어떻게 해야 할까요? 서버를 10대를 사용하면 됩니다. 그런데 누군가 소프트웨어를 개선해서 초당 20개로 처리할 수 있게 만들었다면 서버를 5개로 줄일 수 있습니다. 비용이 절반으로 줄어든 겁니다.
실제로 LLM 훈련에 드는 비용보다 LLM 서비스에 드는 비용이 훨씬 크다고 합니다. 훈련은 비싸지만 한 번으로 끝인 반면, Inference는 지속적으로 나가고 사용자가 늘수록 늘어나는 비용이기 때문입니다.
이런 이유 때문에 LLM Inference를 빠르게 하기 위한 연구가 활발합니다. 이번 글에서는 Inference 가속을 위한 몇몇 주요 기술들을 살펴보려고 합니다.
왜 느릴까?
해결 방법들을 알기 전에 LLM Inference가 왜 느린지를 먼저 간단히 알아보겠습니다. 문제를 알아야하 해결법도 나오니까요.
너무 크고 계산할 것이 너무 많다
첫 번째 이유는 명확합니다. 모델이 너무 크고 그래서 계산할 것이 너무 많기 때문입니다.
온디바이스에 주로 쓰이는 모델들도 파라미터가 10억에서 30억 개에 이르고, 서버급 모델들은 수백억 개에서 수천억 개에 이릅니다. Neural Net 특성상 모든 파라미터에 대해서 곱셈과 덧셈이 이루어지기 때문에 계산해야 하는 양은 파라미터 수에 비례합니다. 모델이 커질수록 계산할 것이 많아지고 모든 계산을 거친 후 결과를 보는 데까지 시간이 오래 걸립니다.
하지만 모델을 작게 만들면 품질이 떨어집니다. 모델 크기와 품질은 trade off 관계죠.
Self Attention
두 번째 이유는 Transformer 아키텍처 때문에 생깁니다. Transformer 아키텍처의 최대 강점은 Self Attention 구조입니다. Self Attention을 통해 입력 전체에 대한 문맥을 이해할 수 있고, 이를 통해 문맥에 맞는 결과를 생성할 수 있습니다. 다만 문제는 Self Attention에 들어가는 연산량이 매우 많다는 점입니다.
Self Attention에 필요한 연산량은 입력 길이에 제곱으로 늘어납니다. 예를 들어 입력 토큰이 10일 때 필요한 연산량이 100이라면, 입력 토큰이 100이 되면 필요한 연산량은 10,000이 됩니다. 입력은 10배가 됐는데, 연산은 100배가 됐습니다.
Auto Regressive
세 번째는 현대의 LLM들이 Auto Regressive 한 방식으로 작동하는 점입니다. Auto Regressive 방식은 출력이 다시 입력이 돼서 다음 출력을 생성하는 방법을 의미합니다. 예를 살펴보겠습니다.
- 입력으로 "우리나라 수도는 어디야?"라고 넣습니다.
- 모델은 다음 단어로 "대한민국의"를 생성합니다.
- 생성된 결과를 붙여서 "우리나라 수도는 어디야? 대한민국의"를 모델에 넣습니다.
- 모델은 "수도는"을 생성합니다.
- 생성된 결과를 붙여서 "우리나라 수도는 어디야? 대한민국의 수도는"을 모델에 넣습니다.
- 모델은 "서울입니다."를 생성합니다.
- 생성된 결과를 붙여서 "우리나라 수도는 어디야? 대한민국의 수도는 서울입니다."를 모델에 넣습니다.
- 모델은 "<문장끝>"을 생성합니다.
- 생성을 마치고 "우리나라 수도는 어디야? 대한민국의 수도는 서울입니다."를 결과로 출력합니다.
이 예에서 보는 것처럼 LLM들은 생성된 결과를 입력 뒤에 붙이고, 그 입력에 대한 결과를 생성하는 작업을 반복합니다.
Auto Regressive에는 Inference 속도 관점에서 두 가지 문제가 있습니다.
첫 번째는 한 토큰씩 생성을 반복하기 때문에 생성하려는 결과의 길이만큼 시간이 길어진다는 점입니다. LLM을 사용할 때 전체 걸리는 시간이 프롬프트 길이보다 생성되는 출력 길이에 영향을 많이 받는 이유입니다.
두 번째는 Self Attention과 관련이 있습니다. LLM이 근본적으로 하는 일은 주어진 입력 다음에 이어질 가장 가능성이 높은 토큰을 예측하는 것입니다. 입력이 Transformer의 각 단계(Tokenizer, Embedding, Self Attention, FNN 등)를 거치면서 수치로 표현되고, 이 수치를 기반으로 다음에 올 법한 가장 그럴듯한 토큰을 선택합니다. 입력이 거치는 각 단계 중 가장 핵심이 되고, 시간이 오래 걸리는 부분이 Self Attention 계산입니다.
문제는 Auto Regressive 방식 때문에 Self Attention 계산을 중복으로 해야 하는 경우가 많이 생긴다는 점입니다. 앞의 예제를 다시 가져와보겠습니다.
- 입력으로 "우리나라 수도는 어디야?"라고 넣습니다. -> [우리나라의, 수도는, 어디야?]에 대한 Self Attention을 계산합니다. 3 x 3 의 Attention Matrix가 만들어집니다.
- 모델은 다음 단어로 "대한민국의"를 생성합니다.
- 생성된 결과를 붙여서 "우리나라 수도는 어디야? 대한민국의"를 모델에 넣습니다. -> [우리나라의, 수도는, 어디야?, 대한민국의]에 대한 Self Attention을 계산합니다. 4 x 4 의 Attention Matrix가 만들어집니다.
- 모델은 "수도는"을 생성합니다.
직관적으로 왠지 모르게 3단계에서 Self Attention을 계산할 때 1단계에서 이미 계산한 것을 또 계산하고 있는 느낌이 듭니다. 3단계의 총 4 토큰 중 3 토큰이 1단계와 겹치니까요. 시간이 오래 걸리는 똑같은 작업을 반복적으로 하고 있다면 분명히 문제입니다.
방법들
앞에서 이야기한 문제들을 해결하기 위해 많은 노력들이 이어져왔고 그중 몇 가지는 효과가 좋아서 많은 곳에 사용되고 있습니다. 몇가지 대표적인 방법들을 소개해보겠습니다.
이 블로그의 다른 글처럼 이 글도 수식이나 복잡한 아키텍처를 최대한 생략하고 개념적인 설명을 하려고 합니다.
Grouped Query Attention (GQA)
GQA를 이야기하려면 Multi-Headed Attention을 이야기해야 하고, Multi-Headed Attention을 이야기하라면 Self Attention을 이야기해야 합니다. 개념적인 수준에서 하나씩 풀어나가 보겠습니다.
Self Attention
Self Attention은 입력을 구성하는 각 토큰(여기에서는 편의를 위해 단어 또는 어절이라고 가정하겠습니다) 간의 관련성을 수치로 표현한 것입니다. 예를 들어 "매우 아름다운 별 지구에 오신 것을 환영합니다."라는 문장을 살펴보겠습니다. "지구에"와 관련 있는 토큰은 어떤 것들일까요? 느낌적으로 "아름다운", "별"은 관련이 높아 보이고, "매우", "것을", "환영합니다"는 관련성이 낮아 보입니다. 다르게 이야기하면 (지구에, 아름다운), (지구에, 별)의 Attention Score는 크고, (지구에, 매우), (지구에, 것을)의 Attention Score는 작아 보입니다.
- (지구에, 아름다운) : 0.3
- (지구에, 별) : 0.4
- (지구에, 매우) : 0.001
- (지구에, 것을) : 0.0005
같은 식일 수 있겠죠.
Self Attention의 장점은 이렇게 각 토큰 간의 관계를 수치로 표현하기 때문에 각 토큰을 해석할 때 다른 토큰들을 얼마나 고려해야 할지 알 수 있다는 점입니다.
그럼 실제로 Attention Score는 어떻게 계산할까요? 먼저 각 토큰에 대해서 Q(Query), K(Key), V(Value)라는 값을 계산하고, 이 값들의 조합으로 최종 Attention Score를 계산합니다. 실제 계산하는 방법은 뒤에서 한 번 더 다루겠습니다.
중요한 점은 Self Attention을 계산하기 위해서는 중간에 Q, K, V라는 값을 계산해야 한다는 점입니다.
Multi-Headed Attention (MHA)
그런데 이 토큰 간의 관련성이라는 것이 참 모호한 개념입니다. 앞에서는 (지구에, 것을)의 점수가 0.0005로 낮다고 판단했습니다. 아마도 "것을"의 "것"이 지구를 가리키는 것이 아니라 "오신"을 가르키는 것이라고 생각했기 때문일 것입니다.
하지만 다르게 생각해 보면 꼭 그렇지 않을 수 있습니다. "지구"도 명사고, "것"도 명사이기 때문에 품사 간의 관련성은 높다고 볼 수도 있습니다. 이 관점으로 다시 Attention Score를 매겨보겠습니다.
- (지구에, 아름다운) : 0.001
- (지구에, 별) : 0.4
- (지구에, 매우) : 0.001
- (지구에, 것을) : 0.3
지구, 별, 것이 모두 명사이기 때문에 높은 점수를 주었고, 아름다운, 매우는 명사가 아니기 때문에 낮은 점수를 주었습니다. 처음 채점 방식이 토큰 간의 의미적인 관계를 더 중시했다면, 이번 채점 방식은 토큰 간의 문법적인 관계를 더 중시한 셈입니다. 이 외에도 채점 방식은 글자 수, 시제, 토큰 간 거리 등 여러 가지가 될 수 있습니다. 하나의 Self Attention 값으로는 이런 다양한 관점을 모두 표현하기 어려울 수 있습니다.
그래서 등장한 것이 Multi-Headed Attention입니다. Multi-Headed Attention의 아이디어는 간단합니다. Self Attention을 여러 세트를 만들자는 것입니다. 그리고 각 세트를 Head라고 부릅니다. 앞의 예를 다시 살펴보겠습니다.
- Head 1
- (지구에, 아름다운) : 0.3
- (지구에, 별) : 0.4
- (지구에, 매우) : 0.001
- (지구에, 것을) : 0.0005
- Head 2
- (지구에, 아름다운) : 0.001
- (지구에, 별) : 0.4
- (지구에, 매우) : 0.001
- (지구에, 것을) : 0.3
이제 Self Attention이 여러 세트이기 때문에 토큰 간의 다양한 관계를 표현할 수 있어졌습니다.
Self Attention 세트(Head)는 각각의 Q, K, V 를 가집니다. Self Attention을 위해 필요한 Q, K, V와 연산이 늘어났다는 의미입니다.
GQA
MHA를 도입해서 품질은 좋아졌습니다. 하지만 안 그래도 연산량이 많은 Self Attention인데, Self Attention 세트가 늘어났으니 연산량은 더 늘어났습니다.
원래는 이랬던 Q, K, V가
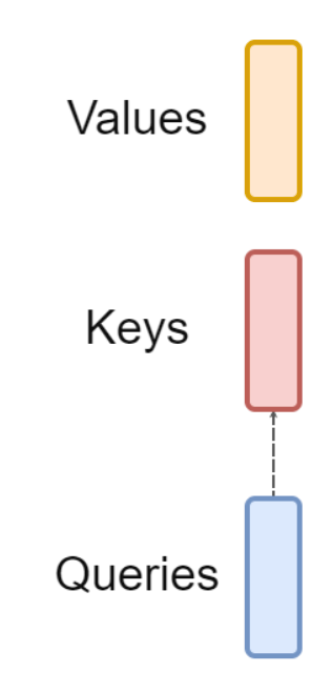
가 이제는
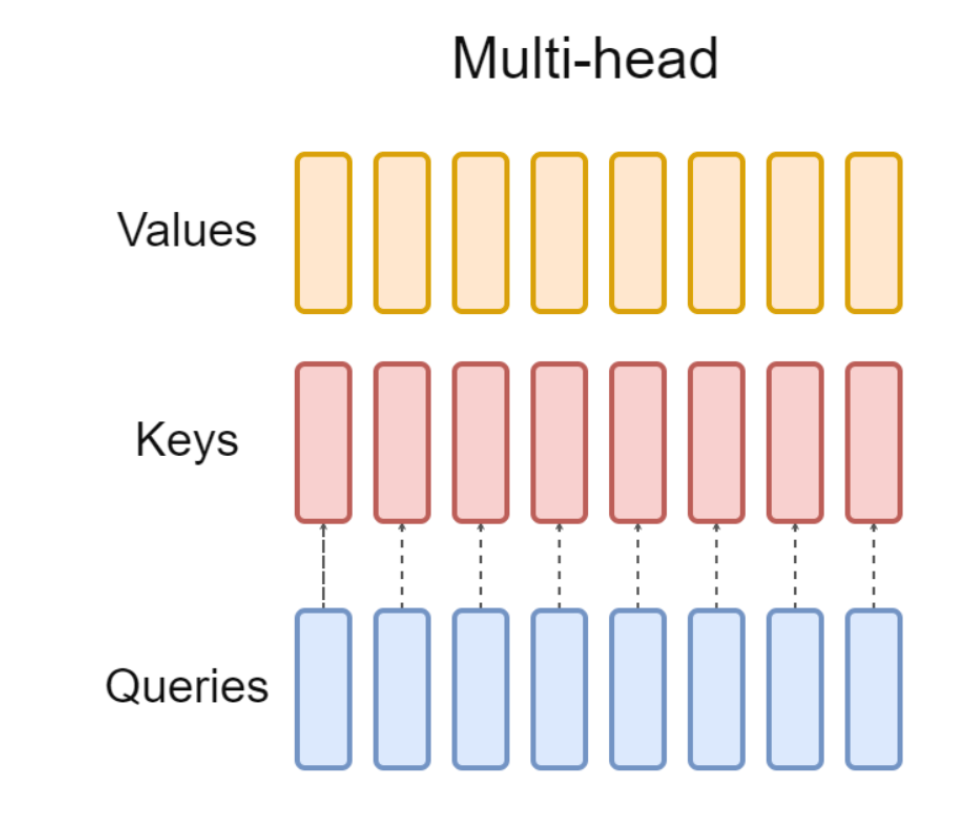
이렇게 여러 세트가 된 것이죠. Head가 늘어나니 머리가 아픕니다.

이때 누군가 아이디어를 냅니다. "Q, K, V 다 따로 만들지 말고 세트마다 Q만 따로 만들고, K, V는 같이 쓰면 안 돼요? Q(Query)만 여러 개니까 Multi-Query Attention(MQA)이라고 부릅시다!"
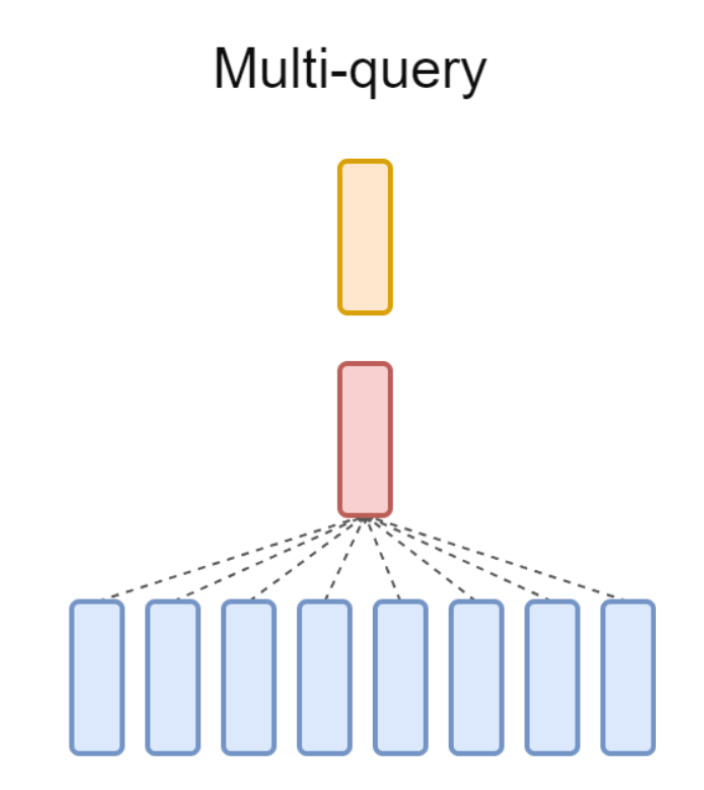
MQA를 도입하자 연산량은 줄어들었지만, 품질이 떨어지는 문제가 발생합니다. 누군가 또 다른 아이디어를 냅니다. "K, V를 전체 공용으로 쓰는 건 너무 심하게 줄인 것 같으니까, 몇 개 세트씩 그룹으로 묶어서 K, V를 같이 씁니다. 그룹으로 묶었으니까 Grouped-Query Attention(GQA)라고 부릅시다!"
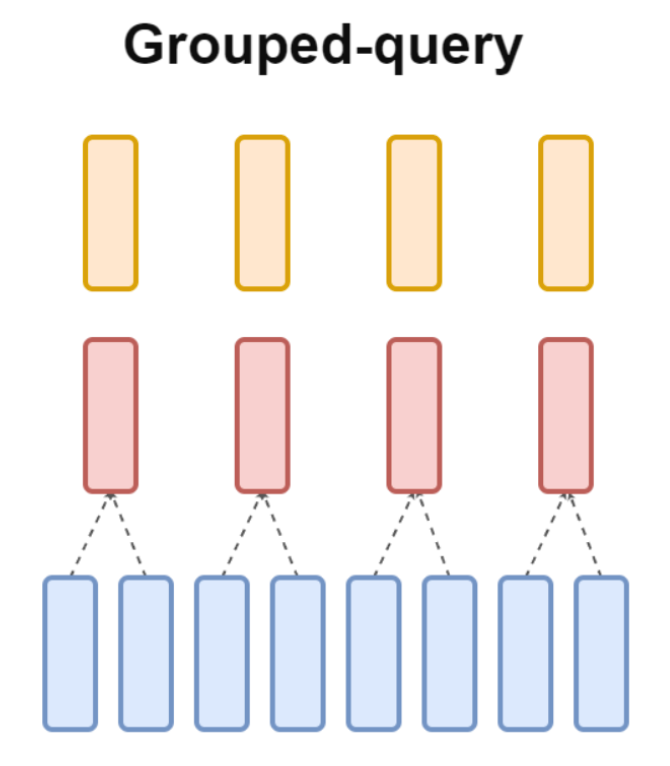
다행히 GQA는 MQA와 달리 원래 MHA에 비해 품질이 많이 떨어지지 않았습니다.
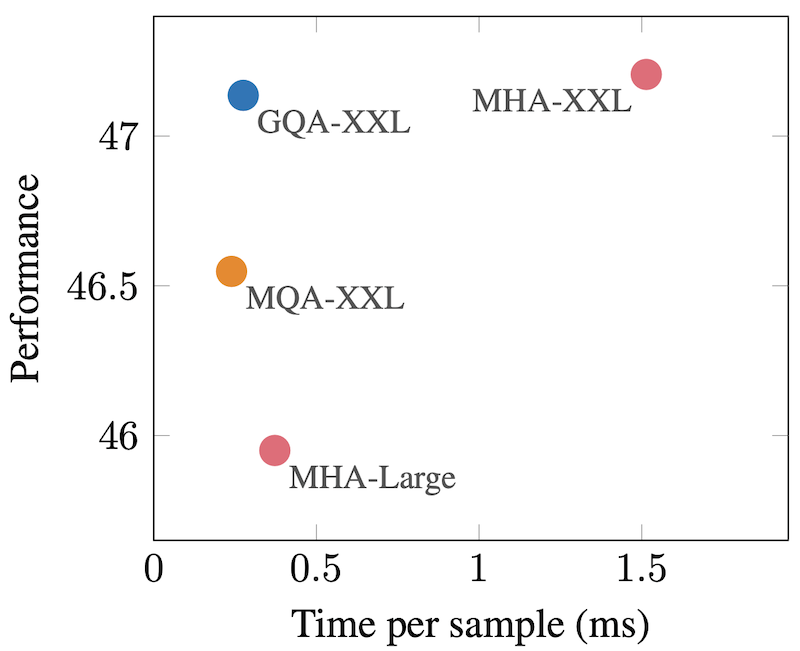
MHA-XXL과 GQA-XXL을 비교해면 걸리는 시간은 1.5ms -> 0.5ms로 줄었지만, 품질은 둘 다 47 정도로 유사한 것을 볼 수 있습니다. 반면 MQA-XXL은 걸리는 시간은 줄었지만, 품질이 MHA-XXL 대비 떨어졌습니다.
참고로 GQA는 구글이 처음 발표했고, LLaMA 2가 본격적으로 사용해서 유명해졌습니다.
Sliding Window Attention (SWA)
SWA도 너무 연산량이 많은 Self Attention의 문제를 해결하려는 방법입니다. 앞에서 설명한 대로 Self Attention은 자신을 포함한 모든 토큰 사이의 관계도를 수치로 표현합니다. 다시 "매우 아름다운 별 지구에 오신 것을 환영합니다."를 살표 보겠습니다.
"매우"라는 토큰은
- (매우, 매우)
- (매우, 아름다운
- (매우, 별)
- (매우, 지구에)
- (매우, 오신)
- (매우, 것을)
- (매우, 환영합니다.)
사이의 점수를 모두 계산합니다. 다음으로 "아름다운"에 대해서도
- (매우, 아름다운)
- (아름다운, 아름다운)
- ...
- (아름다운, 환영합니다.)
사이의 점수를 모두 계산합니다. "매우 아름다운 별 지구에 오신 것을 환영합니다."에 총 7 토큰이 있기 때문에 7 * 7 = 49번의 계산을 해야 합니다. 입력 내의 모든 토큰의 대해 Attention Score를 계산하기 때문에 Global Attention이라고도 부릅니다.
이때 또 누군가 아이디어를 냅니다. "어차피 특정 토큰하고 멀~~리 있는 토큰과는 관계도가 낮을 것 같은데, 근처에 있는 토큰들하고 점수만 계산하면 어때요?" 나쁘지 않아 보입니다. 토큰마다 점수를 계산할 이웃의 크기(Window)를 정하고, 첫 토큰에서부터 시작해서 이 크기만큼 이동(Sliding)하면서 Attention Score를 계산합니다.
예를 들어 Window 크기를 1로 해보겠습니다. 즉, 해당 토큰의 좌우 1 토큰과만 Attention Score를 계산합니다.
- (매우, 매우)
- (매우, 아름다운)
- (아름다운, 매우)
- (아름다운, 아름다운)
- (아름다운, 별)
- (별, 아름다운)
- (별, 별)
- (별, 지구에)
- ...
이렇게 자신을 포함해서 왼쪽 1개, 오른쪽 1개 토큰과 점수만 계산하면 됩니다. 토큰마다 3번만 계산하면 되기 때문에 7 * 3 = 21 (정확히는 처음과 마지막은 1개씩 적기 때문에 19번) 번만 계산하면 됩니다. Global Attention의 49번 대비 엄청나게 적은 숫자입니다.
SWA도 GQA와 같이 품질 저하는 최소화하면서 Attention 계산 속도를 빠르게 할 수 있는 방법으로 널리 사용되고 있습니다. 참고로 SWA는 Longformer라는 논문에서 소개되었고, Mistral이 사용하면서 유명해졌습니다.
KV Cache
KV Cache는 Auto Regressive 방식에서 생기는 비효율(중복 계산)을 줄여보려는 시도입니다. KV Cache를 이해하기 위해서는 Q(Qeury), K(Key), V(Value)를 포함해서 Self Attention이 어떻게 작동하는지 조금 더 깊은 이해가 필요합니다.
앞의 GQA에서 간단히 설명한 대로 Self Attention은 자신을 포함해서 각 토큰 사이의 관계성을 수치(점수)로 표현한 것입니다. Self Attention을 계산하는 방법을 단순화해서 풀어보겠습니다. 예로 "지구는 매우 아름답다."를 사용하겠습니다.
- 각 토큰마다 Q, K, V 값을 계산합니다. (실제 계산은 W_q, W_k, W_v라는 weight matrix를 학습하고 곱해서 계산합니다). 아래 총 9가지 값이 나옵니다.
- Q_지구는, K_지구는, V_지구는
- Q_매우, K_매우, V_매우
- Q_아름답다, K_아름답다, V_아름답다
- "지구는"과 다른 토큰(매우, 아름답다) 사이의 Attention Score를 계산해 보겠습니다.
- 관심 있는 토큰이 Query가 됩니다. 즉, 이 경우에는 지구는이 Q입니다.
- "Q_지구는"과 "K_매우"를 곱합니다. 이 값을 "T_지구는_매우"라고 부르겠습니다.
- "Q_지구는"과 "K_아름답다"를 곱합니다. 이 값을 "T_지구는_아름답다"라고 부르겠습니다.
- "T_지구는_매우"과 "T_지구는_아름답다"를 Normalize 해서 두 값의 합이 1이 되도록 합니다. 각각을 TN_지구는_매우"과 "TN_지구는_아름답다"이라고 해보겠습니다.
(3단계는 우리 논의에서는 중요하지 않으니 무시해도 됩니다) - "TN_지구는_매우"과 "TN_지구는_아름답다"에 각각 "V_매우"와 "V_아름답다"를 곱합니다. 이 값이 Attention Score가 됩니다. 예를 들어 (지구는, 매우)의 점수는 "TN_지구는_매우 * V_매우"가 됩니다.
- 3번의 복잡한 과정은 참고로만 하고, (지구는, 매우) 사이의 점수를 A(Q_지구는, K_매우, V_매우)라고 간단히 표현해 보겠습니다. 그럼 아래와 같은 Attention Score를 얻을 수 있습니다.
| 지구는 | 매우 | 아름답다 | |
| 지구는 | A(Q_지구는, K_지구는, V_지구는) | A(Q_지구는, K_매우, V_매우) | A(Q_지구는, K_아름답다, V_아름답다) |
| 매우 | A(Q_매우, K_지구는, V_지구는) | A(Q_매우, K_매우, V_매우) | A(Q_매우, K_아름답다, V_아름답다) |
| 아름답다 | A(Q_아름답다, K_지구는, V_지구는) | A(Q_아름답다, K_매우, V_매우) | A(Q_아름답다, K_아름답다, V_아름답다) |
이제 이 방식이 Auto Regressive와 결합됐을 때 어떤 현상이 생기는지 살펴보겠습니다.
아래는 LLM에게 "지구는"을 입력으로 주고 문장을 생성하는 예입니다. 처음에 설명한 대로 아래와 같이 문장이 생성됩니다.
- 모델에 "지구는"을 입력으로 줍니다.
- 모델은 "매우"를 생성합니다.
- 모델에 "지구는 매우"를 입력으로 줍니다.
- 모델은 "아름답다"를 생성합니다.
- 모델에 "지구는 매우 아름답다"를 입력으로 줍니다.
- 모델은 "<문장끝>"을 생성합니다.
각 단계에서 Attention Score를 살펴보겠습니다.
1. 모델에 "지구는"을 입력으로 줍니다. 입력이 "지구는" 밖에 없기 때문에 아래와 같은 Attention Score가 생성됩니다.
| 지구는 | |
| 지구는 | A(Q_지구는, K_지구는, V_지구는) |
이 Attention Score를 기반으로 모델이 "매우"를 생성합니다.
2. 모델에 "지구는 매우"를 입력으로 줍니다. 이 경우에 Attention Score를 보겠습니다.
| 지구는 | 매우 | |
| 지구는 | A(Q_지구는, K_지구는, V_지구는) | 0 |
| 매우 | A(Q_매우, K_지구는, V_지구는) | A(Q_매우, K_매우, V_매우) |
여기에서 중요한 점은 (지구는, 매우)의 점수가 0이라는 점입니다. Masked Self Attention이라는 방식인데요. "지구는"이라는 토큰 입장에서 보면 "매우"라는 토큰은 미래의 토큰입니다. "지구는"이 들어온 순간에 다음 토큰이 무엇인지 알 수 없습니다. 그래서 현재 토큰 이후의 토큰은 강제로 점수를 0으로 지정합니다. 미래 토큰(이후 토큰)을 가린다(Mask)는 의미에서 Masked Self Attention이라고 부릅니다.
이미 이 시점에 비효율의 냄새가 납니다. (지구는, 지구는)의 점수인 A(Q_지구는, K_지구는, V_지구는)가 이미 1단계에서 계산한 (지구는, 지구는)의 점수와 같습니다. 일단 넘어가죠.
이제 모델은 이 Attention Score를 기반으로 "아름답다"를 생성합니다.
3. 모델에 "지구는 매우 아름답다"를 입력으로 줍니다. 이 경우에 Attention Score를 보겠습니다.
| 지구는 | 매우 | 아름답다 | |
| 지구는 | A(Q_지구는, K_지구는, V_지구는) | 0 | 0 |
| 매우 | A(Q_매우, K_지구는, V_지구는) | A(Q_매우, K_매우, V_매우) | 0 |
| 아름답다 | A(Q_아름답다, K_지구는, V_지구는) | A(Q_아름답다, K_매우, V_매우) | A(Q_아름답다, K_아름답다, V_아름답다) |
이제 이 방식이 Auto Regressive와 결합됐을 때 어떤 현상이 생기는지 살펴보겠습니다.
2단계에서와 마찬가지로 "지구는" 입장에서 미래인 "매우"와 "아름답다"는 점수가 0이고, "매우" 입장에서 미래인 "아름답다"는 점수가 0입니다. 0을 제외한 나머지 6칸은 앞에서 설명한 Self Attention 계산 방식에 따라 점수를 계산합니다.
여기까지 오자 비효율과 중복의 냄새가 더 강하게 납니다. (지구는, 지구는), (매우, 지구는), (매우, 매우)의 점수가 이미 1단계와 2단계에서 계산한 값 그대로입니다. 1 단계에서 (지구는, 지구는)의 값을 저장해 두고, 2단계에서 (매우, 지구는), (매우, 매우)의 값을 저장해 두었다면, 3단계에서 (지구는, 지구는), (매우, 지구는), (매우, 매우) 점수를 다시 계산할 필요 없이 그대로 꺼내 쓰기만 하면 됩니다. 즉, 6개 점수를 계산하는 대신 새로 추가된 "아름답다"에 해당하는 3개 점수만 계산하고, 나머지 3개는 이전에 저장해 둔 값을 그대로 가져오면 됩니다.
이 내용을 KV Cache 관점에서 살펴보겠습니다. 각 단계에서 모든 K와 V값을 저장해 두었다고 가정해 보겠습니다.
3단계에서는 "아름답다"와 다른 토큰 사이의 Attention Score를 구해야 합니다.
(아름답다, 지구는) 점수를 구하기 위해서는 A(Q_아름답다, K_지구는, V_지구는)를 계산해야 합니다. "Q_아름답다"는 계산해야 하지만 "K_지구는", "V_지구는"은 이미 1단계에서 계산한 적이 있습니다. 그래서 이 두 값은 다시 계산하지 않고 저장된 값을 꺼내 쓰면 됩니다.
(아름답다, 매우)도 비슷합니다. "K_매우", "V_매우"를 2단계에서 이미 계산했고 저장했기 때문에, 3단계에서는 새로 계산할 필요 없이 저장된 값을 가져다 쓰면 됩니다.
간단히 말하면, KV Cache는 이전 토큰을 생성할 때 이미 계산한 중간값들을 저장했다가 나중에 재사용한다는 아이디어입니다. 한 가지 주의할 점은 KV Cache는 Auto Regressive라는 방식에서 생기는 문제를 해결하기 위한 방법이기 때문에 모든 입력이 한 번에 제공되는 BERT와 같은 모델에서는 사용할 수 없습니다. Decoder 단에서만 사용할 수 있는 방법입니다.
Flash Attention
Flash Attention은 Self Attention의 계산량이 매우 복잡하다는 문제를 해결하려는 또 다른 방법입니다. GQA, SWA가 정확도를 조금 희생하면서 속도를 높이고, KV Cache가 캐시를 사용해 중복 계산을 줄였다면 Flash Attention은 하드웨어의 특성을 활용해서 Self Attention 계산을 빠르게 합니다.
Flash Attention을 이해하기 위해서는 먼저 요즘 GPU가 어떻게 작동하는지를 알아야 합니다.
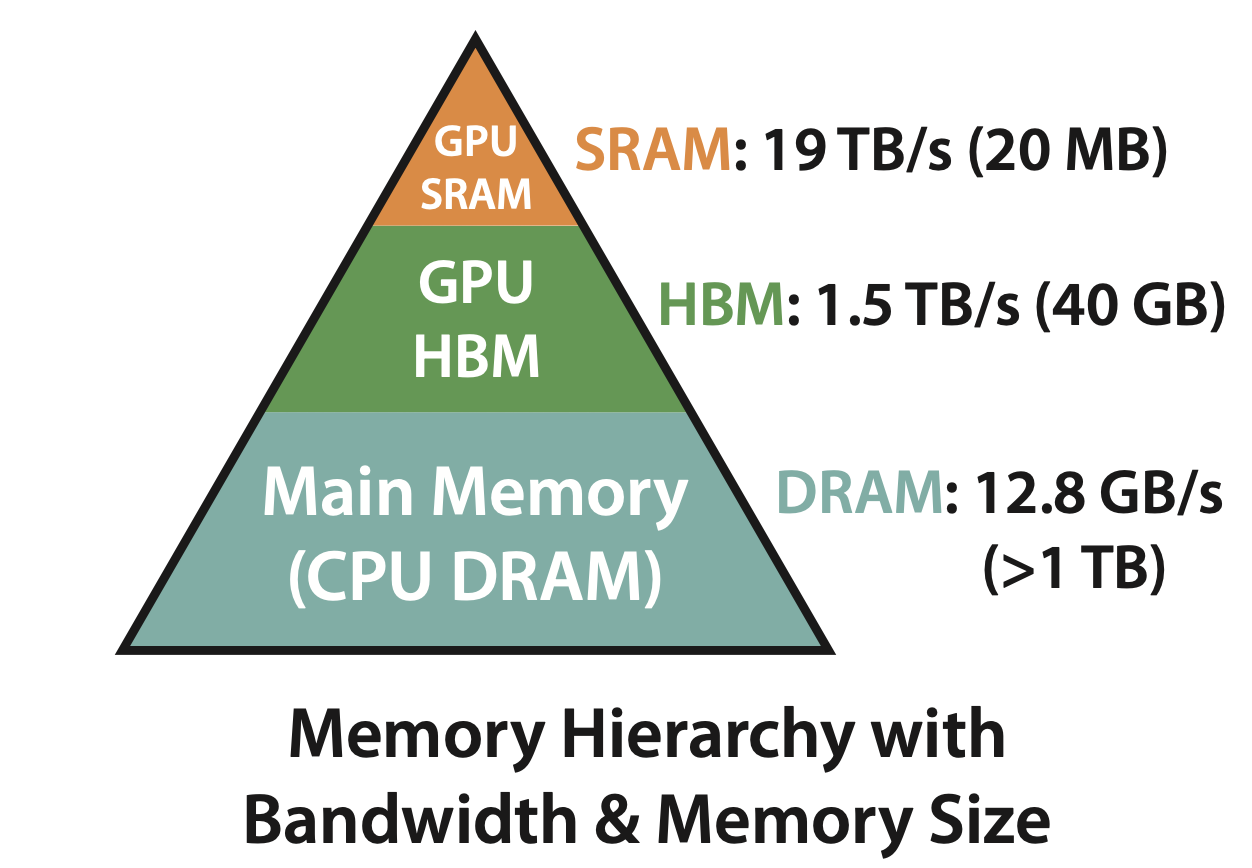
위는 GPU 연산에 쓰이는 메모리가 어떻게 구성되어 있는지를 표현한 그림입니다.
- GPU 코어가 직접 접근하는 메모리는 SRAM이라고 부릅니다. 아주 빠른 대신에 용량도 아주 적습니다. (속도 19TB/s, 용량 20MB)
- GPU의 메인 메모리 격인 HBM은 SRAM보다는 많이 느리지만 대신 용량이 넉넉합니다. (속도 1.5TB/s, 용량 40GB)
- CPU가 사용하는 메모리인 DRAM은 HBM보다 많이 느리고, HBM보다 용량은 훨씬 넉넉합니다. (속도 12.8GB/s, 용량 1TB 이상)
보통 GPU 연산은 아래와 같이 일어납니다.
- 디스크에서 데이터를 읽어서 CPU DRAM에 올립니다.
- CPU DRAM의 데이터를 GPU HBM으로 옮깁니다.
- GPU HBM의 데이터를 SRAM으로 옮깁니다.
- SRAM의 데이터를 사용해 GPU가 계산을 합니다.
- 이 값을 다시 HBM에 저장합니다.
- 연산이 아직 남았다면 3단계-5단계를 반복합니다.
- 연산이 끝났다면 값을 반환합니다.
위에서 볼 수 있는 것처럼 매번 GPU 연산 때마다 값을 HBM에서 읽어와서 계산하고 다시 HBM에 저장합니다. SRAM은 저용량의 귀한 자원이기 때문에 이렇게 할 수밖에 할 수 없습니다. HBM->SRAM->HBM 사이에 데이터를 이동을 위한 지연이 필연적으로 발생합니다.
위 단계를 Q, K, V를 통한 Self Attention 계산에 적용해 보겠습니다.
- Q, K 값을 HBM에서 SRAM으로 읽어옵니다. 두 값을 곱하고 결과를 HBM에 저장합니다.
- 이 값을 다시 HBM에서 SRAM으로 읽어오고 softmax를 계산합니다. 이 값을 HBM에 저장합니다.
- 2번의 값과 V 값을 HBM에서 SRAM으로 읽어옵니다. 두 값을 곱하고 결과를 HBM에 저장합니다.
- 3번의 결과를 반환합니다.
중간 계산들을 HBM->SRAM->HBM에 저장하는 것을 볼 수 있습니다. 만약 HBM->SRAM->HBM 사이에 데이터 복사하는 작업을 줄이고 SRAM에서 최대한 많이 연산을 하면 어떻게 될까요? 당연히 속도가 빨라질 겁니다.
Flash Attention의 아이디어가 저 내용입니다. 그런데 무슨 수로 HBM->SRAM->HBM 간 데이터 이동을 줄일 수 있을까요?
Flash Attention 논문에 자세한 설명이 있지만 간단히 이야기하자면 Flash Attention 개발자들이 원래 Self Attention 구현을 분석해서 SRAM에서 최대한 많은 연산이 일어나도록 CUDA로 재구현했습니다.

위의 그래프를 보면 PyTorch로 구현한 순수한 Self Attention의 Matmul, Mask, Softmax 등의 연산으로 이루어지는데, Flash Attention에서는 이를 모두 합쳐서 Fused Kernel이라는 것을 제공합니다. Fused Kernel은 간단히 생각하면 어러 연산이 하나로 합쳐진 연산이라고 볼 수 있습니다.
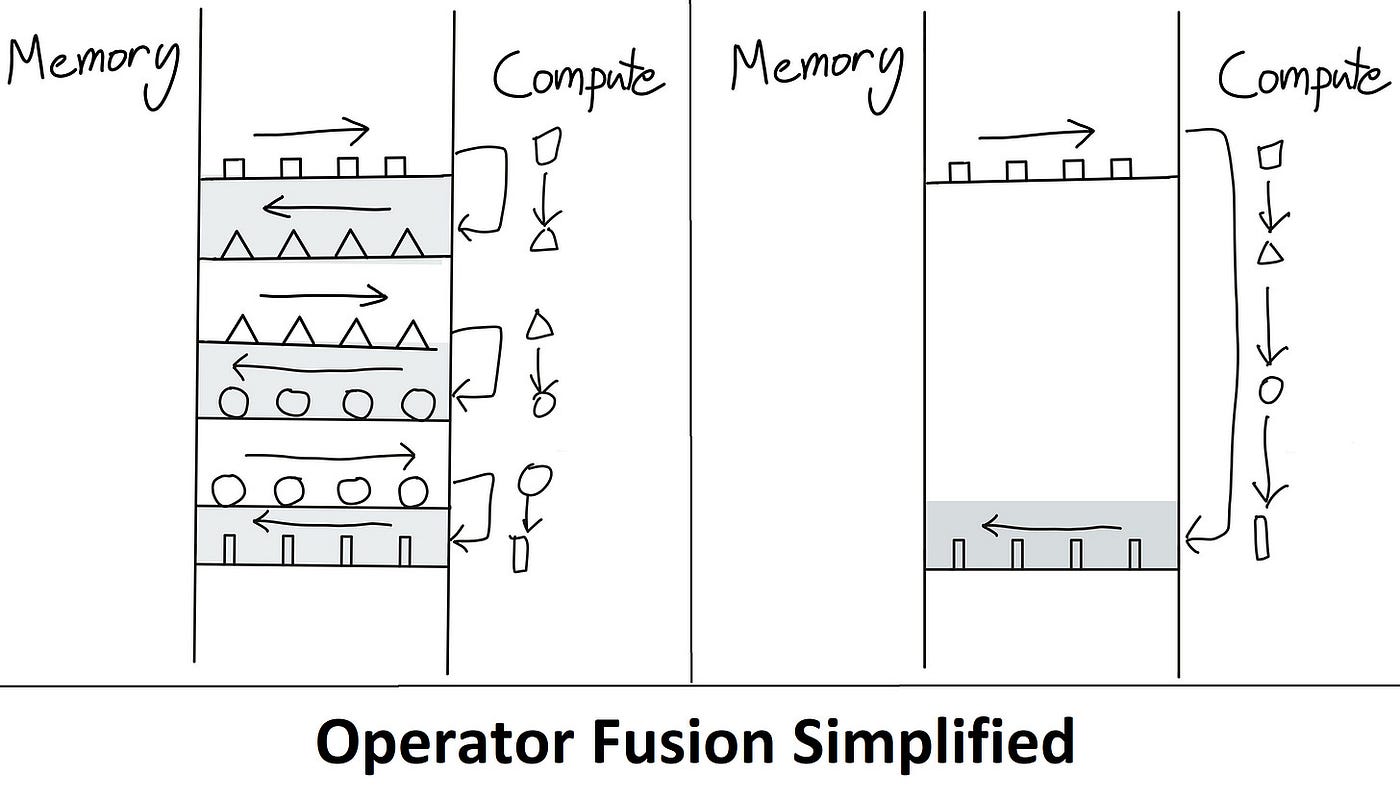
Fused Kernel 연산은 HBM->SRAM->HBM 간 데이터 이동을 최소화하는 형태로 구현되기 때문에 위의 그래프처럼 매우 빠른 속도를 보여줍니다.
Flash Attention이 처음 나왔을 때는 현실적인 문제가 있습니다. Fused Kernel을 구현하기 위해서는 CUDA처럼 PyTorch 보다 저수준에서 구현이 필요하고, 이 구현은 GPU 아키텍처마다 달라질 수 있습니다. 또 그만큼 정확하고 효율적인 구현을 위해 매우 많은 구현 노력이 들어갑니다. Flash Attention이 처음 나왔을 때 V100 같은 GPU가 지원되지 않은 이유이기도 합니다. 하지만 요즘은 huggingface 등에서 이미 구현해서 제공하기 때문에 사용하기 훨씬 쉬워졌습니다.
Speculative Decoding
지금까지 방법들이 Self Attention의 구조적인 특징을 이용해서 Self Attention 계산 속도를 빠르게 하는 방향이었다면, Speculative Decoding을 새로운 접근법을 취하고 있습니다.
Speculative Decoding의 아이디어는 이렇습니다.
- 실제 사용하려고 하는 느리고 큰 모델보다 빠르고 작은 모델을 선택합니다. 작은 모델은 보통 draft model이라고 부릅니다.
- 작은 모델이 특정 길이만큼 결과를 생성하게 합니다. 모델 크기가 작기 때문에 속도가 빠릅니다.
- 작은 모델이 생성한 결과를 큰 모델에게 주고 생성된 각 토큰이 맞는지 틀린 지 판단하게 합니다.
- 모든 토큰이 맞았다면 작은 모델이 생성한 결과를 사용합니다.
- 만약 틀린 토큰이 있다면 그 토큰부터는 큰 모델의 결과를 Greedy Decoding 해서 사용합니다.
다르게 이야기하면 생성은 작은 모델이 하고, 큰 모델은 채점(+ 필요한 경우에만 생성)을 한다는 방식입니다.
Speculative Decoding이 왜 효과가 있는지에 대해서 먼저 알아보겠습니다.
첫 번째 가정은 어떤 토큰은 상대적으로 생성하기 쉽고, 어떤 토큰은 어렵다는 점입니다. 예를 들어 "나는 어제 밥을" 다음에 이어질 단어는 "먹었다"일 가능성이 매우 높습니다. 예측하기 쉽죠. "안중근의 고향은" 다음에 이어질 단어는 무엇일까요? 정답은 "황해도 해주부 광석동"입니다. 어렵죠. LLM도 마찬가지입니다. 작은 모델이더라도 "나는 어제 밥을" 다음이 "먹었다"라는 것은 정확히 생성할 수 있지만, "안중근의 고향은" 다음이 "황해도 해주부 광석동"이라는 것을 생성하기 위해서는 큰 모델이 필요합니다.
다르게 이야기하면 모든 생성에 항상 큰 모델을 쓸 필요가 없다는 의미이기도 합니다. 쉬운 생성에는 작은 모델을 사용하고, 어려운 생성에만 큰 모델을 사용하면 종합적으로 빠르게 결과를 만들어낼 수 있습니다.
두 번째는 Auto Regressive 생성은 오래 걸리지만 텍스트에 대한 판정은 상대적으로 빠르다는 점입니다. 예를 들어 "아름다운 별 지구에"에 이어지는 문장을 생성한다고 가정해 보겠습니다. 정답은 "아름다운 별 지구에 오신 여러분을 환영합니다."이고요.
큰 모델을 사용한다면 Auto Regressive 특성상 오신, 여러분을, 환영합니다, <문장끝>을 생성해야 합니다. 큰 모델을 총 4번 돌려야 하죠. 한 번에 20ms가 걸린다고 치면 80ms가 걸립니다.
"아름다운 별 지구에 오신 여러분을 환영합니다."을 입력으로 주고 다음 토큰을 생성하게 해 보겠습니다. 예를 들어 "저도"라는 토큰이 생성됐다고 가정해 보죠. "저도"라는 토큰 하나만 생성했기 때문에 20ms만 걸렸습니다. 보통 Decoding 때는 새 토큰에 대한 확률만 신경 쓰지만, "저도"라는 새 토큰을 생성하는 과정에 부수적으로 입력의 각 토큰 즉, 아름다운, 별, 지구에, 오신, 여러분을, 환영합니다 각각에 대한 확률도 계산됩니다. 그리고 이 과정은 "저도"를 생성하는 20ms 안에 포함되기 때문에 매우 빠릅니다.
이제 이 토큰별 확률을 사용하면 작은 모델이 생성한 오신, 여러분을, 환영합니다가 정말 큰 모델 관점에서 봤을 때 정답인지 아닌지 알 수 있습니다. 다른 방법으로는 큰 모델의 결과를 Greedy Decoding 해서 실제 토큰으로 만들고, 이 토큰들을 작은 모델의 생성결과와 비교할 수도 있습니다.
작은 모델이 토큰 하나를 생성하는데 5ms가 걸렸다고 가정해 보겠습니다. 오신, 여러분을, 환영합니다, <문장끝> 의 4 토큰을 생성하는데 20ms가 걸렸고, 큰 모델을 통한 판정에는 20ms가 걸렸습니다. 총 40ms가 걸렸습니다. 큰 모델만 사용한 경우인 80ms과 비교해보면 ㅈ절반만 걸린 것을 알 수 있습니다.
여기에서 조금 더 최적화를 할 수도 있습니다. 우선 판정 과정에서 사용한 새 토큰을 다음 생성 결과로 사용하면 20ms를 아낄 수 있습니다. 또, 작은 모델이 특정 길이를 전부 생성하기를 기다리지 않고, 한 토큰 생성할 때마다 병렬로 큰 모델을 돌려서 판정을 할 수도 있습니다.
Speculative Decoding을 보여주는 좋은 비디오가 있어서 가져와 봤습니다. 출처는 Google입니다.
(https://research.google/blog/looking-back-at-speculative-decoding/)
Speculative Decoding이 제대로 잘 작동하려면 작은 모델 (draft model)의 품질이 중요합니다. 빠르기만 해서는 안 됩니다. 작은 모델이 생성한 결과가 매번 틀리다면 결국 큰 모델을 통해 다시 생성해야 하고, 결국 작은 모델을 돌리는데 불필요한 시간만 쓴 셈이 되기 때문입니다.
최근에는 Self Speculative Decoding이 제안되기도 했습니다. 원래 Speculative Decoding이 작은 Draft Model과 큰 Verfication Model을 사용하는 반면 Self Speculative Decoding은 큰 모델 하나만 사용합니다. 큰 모델 전체를 돌리지 않고 모델의 일부 레이어만 사용해서 Draft Model로 사용하고, 전체 레이어를 돌려서 Verification Modely로 사용하는 방식입니다.
마무리
글을 처음 시작할 때는 LLM Inference 가속을 위한 대표적인 몇 가지 기술을 간단히 소개하려고 했는데 쓰다 보니 Attention에 대해서도 이야기하고 글 자체도 길어졌습니다.
최대한 복잡한 수식을 피하고 개념 수준에서 설명하려고 노력했는데 잘 전달이 됐는지 모르겠습니다. 한편으로는 그러다 보니 자세하지 않고 너무 추상적인 설명에서 그친 느낌도 있고요. 부디 조금이나마 관련 기술을 이해하시는데 도움이 됐으면 하는 바람입니다.
'Deep Learning' 카테고리의 다른 글
| LLM: Pretrained vs Instruction Tuned Model (2) | 2024.10.27 |
|---|---|
| LLM : On-Device LLM (2) | 2024.08.29 |
| LLM : Token (2) | 2024.06.10 |
| LLM : Context Window (1) | 2024.05.25 |
| LLM : RAG (3) | 2024.04.28 |